| Главная » Статьи » Компьютеры » Базы данных |
Четвертая нормальная форма
Рассмотрим таблицу R (Subj, Teach, Book), где Subj – учебный предмет, Teach- преподаватель по этому предмету, Book – книга, рекомендуемая преподавателем Teach для изучения предмета Subj. Приведем пример заполнения таблицы R.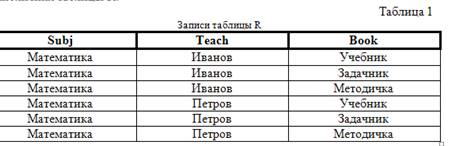 Единственным ключом таблицы R является совокупность всех трех полей. Использование определенным преподавателем некоторой книги может быть показано только наличием соответствующей записи в таблице. Предположим, что преподавание математики в данном учебном заведении строго предполагает использование именно этих трех книг. В случае приема на работу преподавателя Сидорова придется дополнять таблицу тремя записями. Если же руководство примет решение об обязательном использовании еще одной книги, то потребуется по каждому преподавателю вносить еще одну . Можно избежать этих неудобств, разложив отношение R на два отношения R1 (Subj, Teach) и R2 (Subj, Book), имеющих две и три записи соответственно. Тогда при включении нового преподавателя добавится единственная запись в таблицу R1, а при расширении списка книг потребуется дополнить таблицу R2 одной записью. Такая декомпозиция отношения R называется разложением без потерь. В этом примере мы имеем дело с многозначными зависимостями атрибутов Teach и Book от атрибута Subj, которые обозначаются двойной стрелкой, то есть Subj » Teach и Subj » Book. При многозначной зависимости совокупностей атрибутов X и Y (X » Y) каждое значение X определяет множество значений Y, которое не зависит от других атрибутов отношения. Пока это только пояснение, а не строгое определение. Непонятно, что значит "не зависит от других атрибутов отношения”. Строгое определение будет дано позже. Функциональная зависимость является частным случаем многозначной зависимости. Допустим сейчас, что преподавание математики менее стандартизовано. Пусть, например, преподаватель Петров не использует методички, то есть таблица R содержит только первые пять записей. При декомпозиции на отношения R1 и R2 у нас ничего не изменится, то есть окажется невозможным установить потерю одной записи в таблице R. Такая декомпозиция называется разложением c потерей информации, что, естественно, недопустимо. Оказывается, что в этом случае многозначные зависимости отсутствуют, то есть атрибуты Teach и Book взаимозависимы. Может показаться, что другой вариант разложения отношения R на отношения R1 (Subj, Teach) и R3 (Teach, Book) решает все проблемы. Это не так. Если преподаватель ведет несколько предметов, то невозможно понять связь книг с предметами. Рассмотрим еще один пример. Пусть сейчас таблица R (City, Day, Model) содержит сведения о самолетных рейсах и имеет следующий вид. 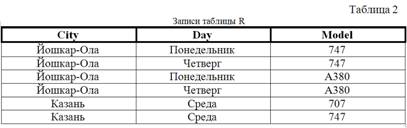 Отношение R разлагается без потерь на два отношения R1 (City, Day) и R2 (City, Model), показанные в таблицах 3 и 4. 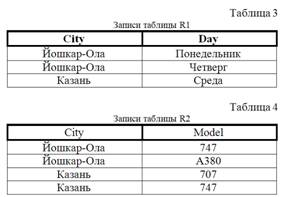 Если же удалить рейс (Йошкар-Ола, Понедельник, A380) из таблицы R, то таблицы R2 и R3 не изменятся, но это уже будет разложение с потерями. Дадим строгое определение многозначной зависимости [4]. Пусть в отношении R имеются два множества атрибутов X и Y. Обозначим через Z оставшиеся атрибуты отношения R, то есть Z = R - (X, Y). Множество атрибутов Y отношения R многозначно зависит от множества атрибутов X ( X » Y), если для любых двух кортежей (x1, y1, z1) и (x1, y2, z2) в отношении существуют также кортежи (x1, y1, z2) и (x1, y2, z1). Для практики важны случаи, когда возможно разложение отношения без потерь, поэтому из рассмотрения исключают так называемые тривиальные многозначные зависимости. Многозначную зависимость называют тривиальной, если множество атрибутов X включает в себя множество атрибутов Y либо X и Y охватывают все атрибуты отношения. Функциональная зависимость также относится к тривиальным многозначным зависимостям Доказано, что нетривиальные многозначные зависимости от одного и того же множества атрибутов всегда бывают парными, то есть если X » Y, то и X » Z. Поэтому их часто представляют вместе в виде X »Y | Z. Разложение отношения R (X, Y, Z) без потерь на R1 (X, Y) и R2 (X, Z) возможно только в случае наличия многозначных зависимостей X » Y и X » Z. В первом примере с отношением R (Subj, Teach, Book) имелись многозначные зависимости Subj » Teach и Subj » Book. После удаления последней записи многозначных зависимостей не осталось. Действительно, рассмотрим кортежи (Математика, Иванов, Методичка) и (Математика, Петров, Учебник). Кортежа (Математика, Петров, Методичка) в отношении уже нет, что показывает отсутствие многозначной зависимости. В примере с рейсами после удаления третьей записи рассмотрим кортежи (Йошкар-Ола, Понедельник, 747) и (Йошкар-Ола, Четверг, A380). Снова запись (Йошкар-Ола, Понедельник, A380) отсутствует. Значит, многозначной зависимости нет, и разложение без потерь невозможно. Есть несколько эквивалентных определений четвертой НФ. Дадим наиболее понятное из них в практическом плане. Отношение находится в четвертой НФ, если оно находится в НФБК, и отсутствуют нетривиальные многозначные зависимости, то есть все многозначные зависимости фактически представляют собой функциональные зависимости от ключей отношения. На практике приведение к четвертой НФ встречается редко. Наличие многозначных зависимостей устанавливаются по смыслу информации, а не формальному определению. Разложение без потерь возможно, если Y и Z в прежних обозначениях не имеют взаимного влияния. Приведем в заключение некоторые важные аспекты, связанные с нормализацией БД. 1. Наряду с очевидными достоинствами нормализация имеет и нежелательные эффекты. Увеличение числа таблиц уменьшает наглядность восприятия информации, увеличивает трудоемкость запросов за счет установления связи таблиц. Для достижения наглядности разрабатывают программным образом удобные для пользователя формы предъявления информации, а также используют представления (виртуальные таблицы, заполняемые в процессе вычислений). Для снижения трудоемкости большие усилия прилагаются в области оптимизации запросов. 2. Нормализации подлежит логическая структура БД, а не физическое представление данных. Характер зависимостей определяет семантика (смысл) данных. 3. В качестве основного метода нормализации рассмотрена декомпозиция таблиц. При большом количестве атрибутов и неочевидном характере зависимостей процесс декомпозиции отличается высокой трудоемкостью и сложностью. Для преодоления этих недостатков разработан алгоритм синтеза [4]. Этот метод помимо сложности не гарантирует получение НФБК, но приводит к так называемым LTK-нормальным формам. Источник: Четвертая нормальная форма | |
| Просмотров: 2409 | Комментарии: 1 | Теги: | Рейтинг: 5.0/1 |
| Всего комментариев: 1 | ||
| ||